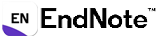Peta Penelitian SEIRS-Vaksin COVID-19: Analisis Tren, Temuan, dan Tantangan Model Matematika

Muhamad Fahri Fauzan; Alya Ramadhani; Dara  Maywanti; Aban Subanul Fahmi; Bayu Sukmaangara

Penulis

Muhamad Fahri Fauzan Universitas Islam Negeri Siber Syekh Nurjati Cirebon Penulis
Alya Ramadhani Universitas Islam Negeri Siber Syekh Nurjati Cirebon Penulis
Dara Maywanti Universitas Islam Negeri Siber Syekh Nurjati Cirebon Penulis
Aban Subanul Fahmi Universitas Islam Negeri Siber Syekh Nurjati Cirebon Penulis
Bayu Sukmaangara Universitas Islam Negeri Siber Syekh Nurjati Cirebon Penulis

Kata Kunci:

Model SEIRS, Vaksinasi COVID-19, Kontrol Optimal, Model Orde Fraksional, Asimilasi Data

Abstrak

Pengendalian pandemi COVID-19 membutuhkan model matematika yang mampu mengakomodasi dinamika imun yang kompleks, terutama fenomena penurunan imunitas dan intervensi vaksinasi. Studi ini melakukan Tinjauan Literatur Sistematis menggunakan protokol PRISMA untuk memetakan tren, temuan, dan tantangan metodologis dalam pemodelan SEIRS-Vaksinasi. Dari 80 artikel yang diidentifikasi pada tahap awal, 56 artikel memenuhi kriteria inklusi dan dianalisis. Selanjutnya, 11 artikel dipilih melalui teknik pengambilan sampel bertujuan sebagai sampel representatif untuk analisis komparatif mendalam dari lima kategori metodologi utama: Deterministik (ODE), Kontrol Optimal, Orde Fraksional, Asimilasi Data/Stokastik, dan Spasial. Hasil sintesis literatur mengungkapkan pergeseran paradigma yang signifikan dari model deterministik klasik yang berfokus pada analisis stabilitas statis menuju model yang lebih adaptif. Secara khusus, studi ini mengidentifikasi penggunaan Ensemble Kalman Filter untuk estimasi parameter dinamis dan Teori Kontrol Optimal untuk strategi alokasi sumber daya sebagai tren metodologis yang dominan. Temuan model secara konsisten memvalidasi bahwa tingkat vaksinasi adalah parameter intervensi yang paling sensitif, tetapi efektivitas jangka panjangnya sangat bergantung pada durasi kekebalan. Studi ini menyimpulkan perlunya mengembangkan model hibrida yang mengintegrasikan pendekatan stokastik dan kontrol optimal untuk menghasilkan rekomendasi kebijakan yang lebih tepat di masa mendatang.

Unduhan

Data unduhan tidak tersedia.

Biografi Penulis

Bayu Sukmaangara, Universitas Islam Negeri Siber Syekh Nurjati Cirebon

Jurusan Matematika

Referensi

[1] M. A. Misri, K. H. Qadr, and M. A. Rahmatullah, “SEIR Mathematical Model with the Use of Hand Sanitizers to Prevent the Spread of COVID-19 Disease,” CAUCHY J. Mat. Murni Dan Apl., vol. 9, no. 1, pp. 138–154, May 2024, doi: 10.18860/ca.v9i1.25754.

[2] Y. A. Terefe and T. A. Tegegn, “Contribution of the 2021 COVID-19 Vaccination Regime To COVID-19 Transmission and Control in South Africa: A Mathematical Modeling Perspective,” 2024, SSRN. doi: 10.2139/ssrn.5025247.

[3] Y. Hou and H. Bidkhori, “Multi-feature SEIR model for epidemic analysis and vaccine prioritization,” PLOS ONE, vol. 19, no. 3, p. e0298932, Mar. 2024, doi: 10.1371/journal.pone.0298932.

[4] Y. Hou and H. Bidkhori, “Multi-feature SEIR model for epidemic analysis and vaccine prioritization,” PLOS ONE, vol. 19, no. 3, p. e0298932, Mar. 2024, doi: 10.1371/journal.pone.0298932.

[5] N. Nadia et al., “Data-Driven Generating Operator in SEIRV Model for COVID-19 Transmission,” Commun. Biomath. Sci., vol. 6, no. 1, pp. 74–89, July 2023, doi: 10.5614/cbms.2023.6.1.6.

[6] N. Saidi and A. Radid, “Dynamics of a fractional order SEIRS epidemic model with vaccination and nonlinear incidence rates,” Sci. Afr., vol. 29, p. e02825, Sept. 2025, doi: 10.1016/j.sciaf.2025.e02825.

[7] M. S. P. Pramudito and B. P. Prawoto, “Model SEIR Penyakit COVID-19 dengan adanya Migrasi dan Pemberian Vaksin,” MATHunesa J. Ilm. Mat., vol. 9, no. 2, pp. 260–267, Aug. 2021, doi: 10.26740/mathunesa.v9n2.p260-267.

[8] Q. Sun, T. Miyoshi, and S. Richard, “Analysis of COVID-19 in Japan with extended SEIR model and ensemble Kalman filter,” J. Comput. Appl. Math., vol. 419, p. 114772, Feb. 2023, doi: 10.1016/j.cam.2022.114772.

[9] I. F. Y. Tello, A. V. Wouwer, and D. Coutinho, “State estimation of the time–space propagation of COVID-19 using a distributed parameter observer based on a SEIR-type model,” J. Process Control, vol. 118, pp. 231–241, Oct. 2022, doi: 10.1016/j.jprocont.2022.08.016.

[10] C. Bounkaicha and K. Allali, “Stability analysis of reaction–diffusion fractional-order SEIR model with vaccination and saturated incidence rate,” Partial Differ. Equ. Appl. Math., vol. 13, p. 101069, Mar. 2025, doi: 10.1016/j.padiff.2024.101069.

[11] A. El Alami Laaroussi, A. El Bhih, and M. Rachik, “Optimal vaccination and treatment policies with constrained inequalities to study limited vaccination resources for a multistrain reaction–diffusion S E I R model of COVID-19,” Partial Differ. Equ. Appl. Math., vol. 10, p. 100684, June 2024, doi: 10.1016/j.padiff.2024.100684.

[12] J. Ilnytskyi and T. Patsahan, “Compartmental and cellular automaton $SEIRS$ epidemiology models for the COVID-19 pandemic with the effects of temporal immunity and vaccination,” Dec. 07, 2021, arXiv: arXiv:2112.02661. doi: 10.48550/arXiv.2112.02661.

[13] R. C. Poonia, A. K. J. Saudagar, A. Altameem, M. Alkhathami, M. B. Khan, and M. H. A. Hasanat, “An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect,” Life, vol. 12, no. 5, p. 647, Apr. 2022, doi: 10.3390/life12050647.

[14] C. Xu, Y. Yu, G. Ren, Y. Sun, and X. Si, “Stability analysis and optimal control of a fractional-order generalized SEIR model for the COVID-19 pandemic,” Appl. Math. Comput., vol. 457, p. 128210, Nov. 2023, doi: 10.1016/j.amc.2023.128210.

[15] R. Pino, V. M. Mendoza, E. A. Enriquez, A. C. Velasco, and R. Mendoza, “An optimization model with simulation for optimal regional allocation of COVID-19 vaccines,” Healthc. Anal., vol. 4, p. 100244, Dec. 2023, doi: 10.1016/j.health.2023.100244.

[16] S. Arshad, S. Khalid, S. Javed, N. Amin, and F. Nawaz, “Modeling the impact of the vaccine on the COVID-19 epidemic transmission via fractional derivative,” Eur. Phys. J. Plus, vol. 137, no. 7, p. 802, July 2022, doi: 10.1140/epjp/s13360-022-02988-x.

[17] N. Nuraini, F. N. Soekotjo, A. Alifia, K. K. Sukandar, and B. W. Lestari, “Assessing potential surge of COVID-19 cases and the need for booster vaccine amid emerging SARS-CoV-2 variants in Indonesia: A modelling study from West Java,” Heliyon, vol. 9, no. 9, p. e20009, Sept. 2023, doi: 10.1016/j.heliyon.2023.e20009.

[18] N. B. Khedher, L. Kolsi, and H. Alsaif, “A multi-stage SEIR model to predict the potential of a new COVID-19 wave in KSA after lifting all travel restrictions,” Alex. Eng. J., vol. 60, no. 4, pp. 3965–3974, Aug. 2021, doi: 10.1016/j.aej.2021.02.058.

[19] G. González-Parra, M. S. Mahmud, and C. Kadelka, “Learning from the COVID-19 pandemic: A systematic review of mathematical vaccine prioritization models,” Infect. Dis. Model., vol. 9, no. 4, pp. 1057–1080, Dec. 2024, doi: 10.1016/j.idm.2024.05.005.

[20] O. Agossou, M. N. Atchadé, and A. M. Djibril, “Modeling the effects of preventive measures and vaccination on the COVID-19 spread in Benin Republic with optimal control,” Results Phys., vol. 31, p. 104969, Dec. 2021, doi: 10.1016/j.rinp.2021.104969.

[21] Y. H. Garcia, S. Diaz-Infante, and J. A. Minjarez-Sosa, “An integrated mathematical epidemiology and inventory model for high demand and limited supplies under uncertainty,” Decis. Anal. J., vol. 14, p. 100543, Mar. 2025, doi: 10.1016/j.dajour.2024.100543.

[22] S. Paul, A. Mahata, U. Ghosh, and B. Roy, “Study of SEIR epidemic model and scenario analysis of COVID-19 pandemic,” Ecol. Genet. Genomics, vol. 19, p. 100087, May 2021, doi: 10.1016/j.egg.2021.100087.

[23] P. Wintachai and K. Prathom, “Stability analysis of SEIR model related to efficiency of vaccines for COVID-19 situation,” Heliyon, vol. 7, no. 4, p. e06812, Apr. 2021, doi: 10.1016/j.heliyon.2021.e06812.

[24] C. Zuo, F. Zhu, and Y. Ling, “Analyzing COVID-19 Vaccination Behavior Using an SEIRM/V Epidemic Model With Awareness Decay,” Front. Public Health, vol. 10, p. 817749, Jan. 2022, doi: 10.3389/fpubh.2022.817749.

[25] M. Manaqib, M. Mahmudi, and R. A. Salsadilla, “Model Matematika COVID-19 dengan Vaksinasi Dua Tahap, Karantina, dan Pengobatan Mandiri,” Limits J. Math. Its Appl., vol. 20, no. 3, p. 255, Nov. 2023, doi: 10.12962/limits.v20i3.14310.

[26] R. C. Poonia, A. K. J. Saudagar, A. Altameem, M. Alkhathami, M. B. Khan, and M. H. A. Hasanat, “An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect,” Life, vol. 12, no. 5, p. 647, Apr. 2022, doi: 10.3390/life12050647.

[27] V. E. Papageorgiou and G. Tsaklidis, “A stochastic particle extended SEIRS model with repeated vaccination: Application to real data of COVID‐19 in Italy,” Math. Methods Appl. Sci., vol. 47, no. 7, pp. 6504–6538, May 2024, doi: 10.1002/mma.9934.

[28] M. E. Baroudi, H. Laarabi, S. Zouhri, M. Rachik, and A. Abta, “Optimal control problem for COVID-19 with multiple time-delays in state and control,” Results Control Optim., vol. 19, p. 100579, June 2025, doi: 10.1016/j.rico.2025.100579.

[29] A. Abbes, A. Ouannas, N. Shawagfeh, and G. Grassi, “The effect of the Caputo fractional difference operator on a new discrete COVID-19 model,” Results Phys., vol. 39, p. 105797, Aug. 2022, doi: 10.1016/j.rinp.2022.105797.

[30] K. Joshi, E. Rumpler, L. Kennedy-Shaffer, R. Bosan, and M. Lipsitch, “Comparative performance of between-population vaccine allocation strategies with applications for emerging pandemics,” Vaccine, vol. 41, no. 11, pp. 1864–1874, Mar. 2023, doi: 10.1016/j.vaccine.2022.12.053.

[31] A. I. Borovkov, M. V. Bolsunovskaya, A. M. Gintciak, V. V. Rakova, M. O. Efremova, and R. B. Akbarov, “COVID-19 Spread Modeling Considering Vaccination and Re-Morbidity,” Int. J. Technol., vol. 13, no. 7, p. 1463, Dec. 2022, doi: 10.14716/ijtech.v13i7.6186.

[32] S. Margenov, N. Popivanov, I. Ugrinova, and T. Hristov, “Differential and Time-Discrete SEIRS Models with Vaccination: Local Stability, Validation and Sensitivity Analysis Using Bulgarian COVID-19 Data,” Mathematics, vol. 11, no. 10, p. 2238, May 2023, doi: 10.3390/math11102238.